Der Knobelthread

[Ziegenpeter]

Dr. Schlaumeier hat dieses Programm geschrieben. Die Frage ist jetzt, wird es sich immer beenden oder gibt es Fälle in denen es ewig läuft?

 

[Serpel]

Die Folge endet nach endlich vielen Schritten immer bei der 20.

Gruß
Serpel

 

[Ziegenpeter]

Die Folge endet nach endlich vielen Schritten immer bei der 20.

Gruß
Serpel

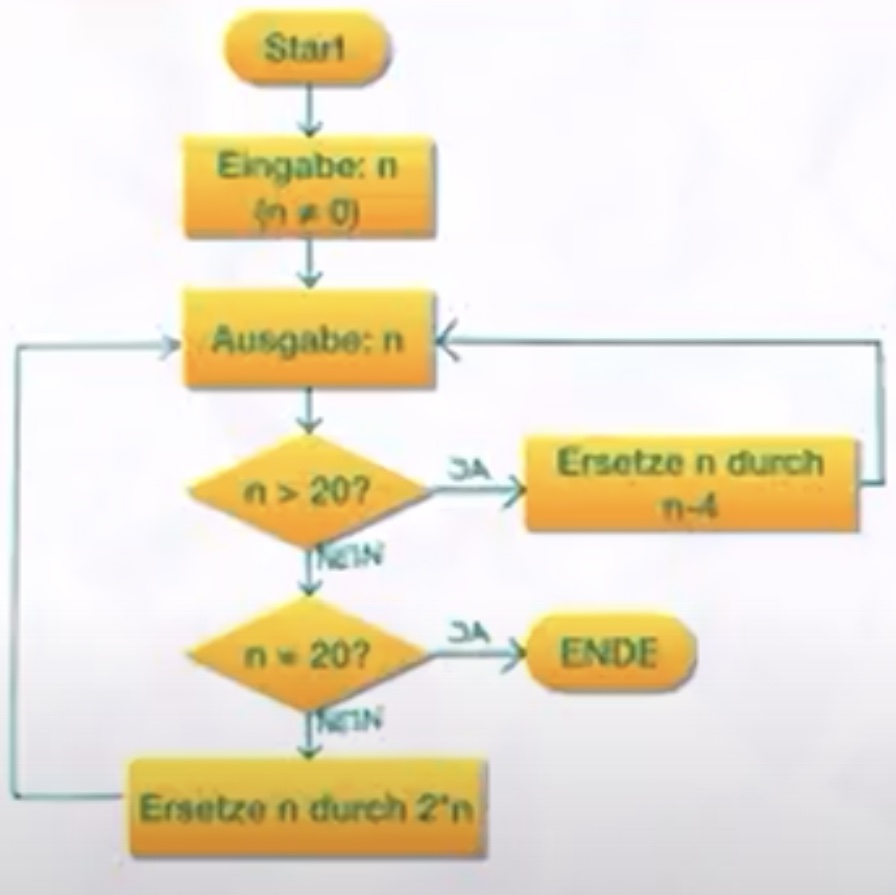
von dir will ich aber den Beweis dafür sehen , danach dein Spiel.

 

[Serpel]

Die Zahl wird ja immer wieder verdoppelt, sobald sie nach sukzessiver Verringerung um 4 unter die 20 kommt (oder bereits ist). Spätestens nach der zweiten Verdoppelung ist sie aber durch vier teilbar (da eine Verringerung um vier nichts an der Teilbarkeit durch zwei ändert) und endet dann in der 20.

Das ist die Beweisidee, die man noch beliebig ausschmücken kann.

Gruß
Serpel

 

[Ziegenpeter]

Dein Spiel

 

[Serpel]

Was ändert sich an der Lösung und an obigem Beweis, wenn man n nicht durch n-4, sondern durch n-8 ersetzt, sobald n > 20 ist?

Gruß
Serpel

 

[Gast 23088]

Nix...

(Edit: Falls richtig, Freispiel!)

 

[Gast 23088]

Mein Problem ist: wie schließe ich (nach der Wahrscheinlichkeitsrechnung) alle unwahrscheinlichen Ziehungen aus?

Serpel hat es ja schon beantwortet. Faires Ziehungsgerät vorausgesetzt gibt es keine unwahrscheinlichen Ziehungen, Du bist dem klassichen Gambler's Fallacy erlegen.

 

[Ziegenpeter]

Was ändert sich an der Lösung und an obigem Beweis, wenn man n nicht durch n-4, sondern durch n-8 ersetzt, sobald n > 20 ist?

Gruß
Serpel

21 13 26 18 36 28 20
22 14 28 20
23 15 30 22 14
24 16 32 24 16 <– Endlosschleife
25 17 34 26 18
26 18
27 19 38 30

 

[Ziegenpeter]

Serpel hat es ja schon beantwortet. Faires Ziehungsgerät vorausgesetzt gibt es keine unwahrscheinlichen Ziehungen, Du bist dem klassichen Gambler's Fallacy erlegen.

gaaaanz falsch, Bill Gates hat eine Formal für unwahrscheinliche Ziehungen gefunden, wie hat er sonst die vielen Milliarden gescheffelt? Die Regierung unterdrückt dieses Wissen nur

 

[Serpel]

16 32 24 16 <– Endlosschleife

Exakt!

Und warum funktioniert dann meine Beweisskizze nicht mehr? (War auch gefragt.)

So oder so - dein Spiel!

Gruß
Serpel

 

[Ziegenpeter]

Exakt!

Und warum funktioniert dann meine Beweisskizze nicht mehr? (War auch gefragt.)

So oder so - dein Spiel!

Gruß
Serpel

Ich bin mir nicht ganz sicher, was du genau hören möchtest.

Deine Beweisskizze fußt darauf, dass jede Zahl spätestens nach 2 maliger Multiplikation mit 2 durch 4 teilbar ist und deshalb durch mehrmaliges Subtrahieren von 4 genau 20 erreicht wird, da 20 durch 4 teilbar ist. 20 ist aber nicht durch 8 teilbar, d.h. sobald du eine Zahl als Startwert nimmst die, sobald sie grösser > 20 wird, durch 8 teilbar ist (mindestens 3 mal den Faktor 2 hat, also z.B. 1, 2, 3, 4, 6, 8, 16, 24 ...) wird das Programm nicht halten.

 

[Ziegenpeter]

Freispiel

 

[nobbe]

so, dann noch mal - nicht, dass sich hier immer nur die 2 professoren unterhalten

 

[Biker-Gina]

Nobbe, das hatten die Herren hier schon - so als kleines Häppchen zwischendurch.

Am besten wieder ein Hochmathematisches Rätsel für die Professoren hier im kleinen Kreis.

 

[Ziegenpeter]

Biker-Gina hat alle verschreckt und jetzt postet niemand mehr?

Also dann das hier: wieviele Blätter fallen gerade sichtbar vom Himmel?

 

[FrankS]

Das ist ja schon fast eine philosophische Frage: Sichtbar für wen? Für mich sind es 5 und damit ist es für mich die richtige Lösung – selbst wenn du mehr oder weniger Blätter siehst

 

[Ziegenpeter]

Ich sehe auch 5, damit hast du das Spiel am Hals oder es geht mit nobbe oben weiter falls da noch unentdeckte Filme im Bild sind

 

[FrankS]

im Filmbild sehe ich noch Captain Future: Die Waschmaschine. Nobbe kann weitermachen, von meiner Seite gibt es Freispiel.

 

[Ziegenpeter]

Wo ist eigentlich Nobbe? Das Leben ohne Knobeleien ist doch sinnlos...

Und da sonst auch niemand will, hier mal eine Frage aus einer großen Boulevardzeitung: Wie unterteile ich ein Quadrat in 4 unterschiedlich große gleichschenklige Dreiecke?

P.S. Serpel darf erst antworten, wenn bis morgen niemand sonst die Lösung bringt, ansonsten ist das wieder in < 1 Minute gelöst...